
โดย ครูปรีณาพรรณ พิมพ์พิศาล
การแทรกสอด 11/23
ดังนั้นจึงพอสรุปได้ว่า
โดยที่ n เป็นตัวเลขแสดงลำดับที่ของแนวปฏิบัพ เริ่มที่ 0, 1, 2, 3, ...
ถ้าเกิดการแทรกสอดแบบหักล้างจะได้ระยะทางแตกต่างคือ
โดยที่ n เป็นตัวเลขแสดงลำดับที่ของแนวบัพ เริ่มที่ 1, 2, 3, ...
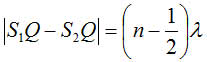
ถ้าเกิดการแทรกสอดแบบเสริมกันจะได้ระยะทางแตกต่างคือ
จากกรณีของบัพจะใช้ค่า n = 1, 2, 3, ... ซึ่งเริ่มจาก 1 ไม่ใช่เลข 0 เหมือนกับกรณีของปฏิบัพ
แต่สามารถเขียนในอีกรูปแบบหนึ่งเพื่อให้ค่า n เริ่มจากเลข 0 เหมือนกับในกรณีของปฏิบัพได้
ดังนี้
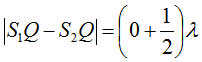
โดยที่ n = 0, 1 ,2, 3, ...
แต่ในที่นี้จะใช้ตามสมการ (5.3-2) เพื่อให้ค่าของ n ในสมการตรงกันกับเลขที่ระบุว่าเป็นเส้นบัพ
ที่เท่าใด
หมายเหตุ ในสมการของกรณีบัพและปฏิบัพจะสังเกตเห็นว่าค่าระยะทางแตกต่างใช้เครื่องหมาย
ค่าสัมบูรณ์ เนื่องจากบางครั้งค่าระยะทางแตกต่างอาจได้ค่าออกมาเป็นลบซึ่งเราจะไม่รวม
เครื่องหมายลบ และเมื่อถอดค่าสัมบูรณ์ออกมาจะเป็นบวกเสมอ
(5.3-3)





ถ้าเกิดการแทรกสอดแบบเสริมกัน
จะได้ระยะทางแตกต่างเท่ากับ
จำนวนเต็มเท่าของความยาวคลื่น



