
โดย ครูปรีณาพรรณ พิมพ์พิศาล
การแทรกสอด 7/23
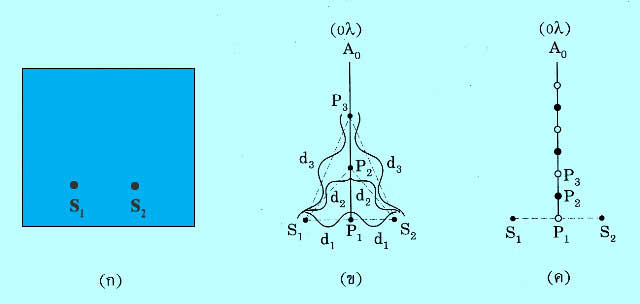
เมื่อเราพิจารณาอย่างละเอียดดังรูป 5.3-8 (ก) แสดงแหล่งกำเนิด S1 และ S2 บนถาดคลื่น
ในขณะที่ยังไม่มีการสร้างคลื่น จะเห็นได้ว่าผิวน้ำไม่มีการกระเพื่อม จากนั้นให้แหล่งกำเนิด
ทั้งสองสร้างคลื่นแล้วพิจารณา การแทรกสอดของคลื่นตามแนวเส้นที่และแนว เริ่มจากแนวเส้น
A0 ซึ่งเป็นเส้นตรงที่แบ่งครึ่ง และตั้งฉากกับเส้นตรงที่เชื่อมระหว่างแหล่งกำเนิดทั้งสอง หรือเป็น
เส้นแนวกลางดังรูป 5.3-8 (ข) ดังนั้นจุดใด ๆ บนแนวเส้นนี้จึงอยู่ห่างจากแหล่งกำเนิดทั้งสอง
เป็นระยะทางเท่ากันเสมอ
รูปที่ 5.3-8 การแทรกสอดบนเส้นปฏิบัพ (ที่มา: พงษ์ศักดิ์ ชินนาบุญ., 2557, หน้า 83)
จากรูป 5.3-8 (ข) นักเรียนจะสังเกตเห็นว่าระยะจาก S1 ไปยังจุด P1 จะมีค่าเท่ากับระยะ
หรือเมื่อพิจารณาจากระยะทางแตกต่างในรูปของจำนวนลูกคลื่นจะพบว่าคลื่นทั้งสองเคลื่อน
ระยะทางแตกต่าง = S1P - S2P = 0 ลูกคลื่น =
หรือยะระจาก S1 ไปยังจุด P2 จะมีค่าเท่ากับระยะจาก S2 ไป P2 ซึ่งมีระยะทางเท่ากับ d2
หรือยะระจาก S1 ไปยังจุด P3 จะมีค่าเท่ากับระยะจาก S2 ไป P3 ซึ่งมีระยะทางเท่ากับ d3
เนื่องจากแนวเส้น A0 แบ่งครึ่งระหว่างแหล่งกำเนิดทั้งสองดังนั้นไม่ว่าเราจะพิจารณาที่จุดใด ๆ
บนแนวเส้น A0 คลื่นจะเคลื่อนที่ได้ระยะทางเท่ากันดังรูป 5.3-8 (ค)
เรียกว่า ความต่างระยะทาง (Path difference) ซึ่งเป็นปริมาณที่
ชี้ให้เห็นว่า ผลต่างของระยะทางที่คลื่นจากแหล่งกำเนิดแต่ละแหล่ง เคลื่อนที่มาถึงจุดหนึ่ง ๆ
ว่าเป็นกี่ลูกคลื่นหรือกี่เท่าของความยาวคลื่น
จาก S2 ไป P1 ซึ่งเป็นระยะทางเท่ากับ d1 เท่ากับความยาวคลื่น
เท่ากับ
เท่ากับ
ที่ได้ระยะทางแตกต่างกันเท่ากับคลื่น 0 ลูก หรือ
แหล่งกำเนิด S1 และ S2 ถึงจุด P ใด ๆ แทนด้วย S1P และ S2P ตามลำดับ จุดบนแนว
เส้นนี้จึงมีเงื่อนไขว่า
เสมอ เมื่อกำหนดให้ระยะทางจาก
ปริมาณ



